Tit-for-Tat
In the prisoner's dilemma, the choices of the two individuals were simple because they interacted only once. If they had been in a situation where there would have been future interactions, they would worry about how their decision would affect the other person's future actions, and as a result, the story might have had a very different ending.
Consider the case of Ingrid and Edward in the table below. Their mother requires them to clean the house each Saturday before they can play. Each has a choice of working hard or loafing. If they both work hard, they can finish in one hour. If they both loaf, the work takes three hours. If one loafs and the other works hard, the job will take an hour and a half. Ingrid ranks the possibilities in the table from best to worst as a, b, c, and d. Edward ranks them in a similar way.
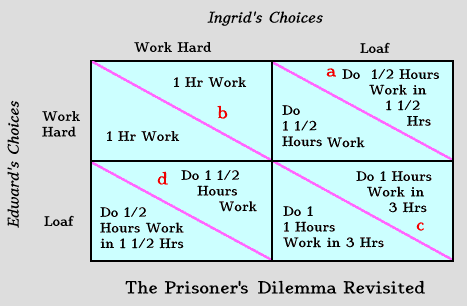
The logic of the prisoner's dilemma suggests that both will loaf. However, because Edward and Ingrid must interact each week, the situation is more complex. One's present actions may influence the other's future actions. Each must see his or her strategy not just in terms of how it affects the payoff this week, but how it will affect the payoffs in the future as well. What one player does will affect the strategy of the other; in turn, this result can affect the strategy of the original player. This chain of decisions coming back to affect future decisions is a case of feedback, and it greatly complicates the problem of deciding strategy.
What strategy should a player choose? Although there is no one best strategy for all circumstances, one that works extremely well over a wide variety of environments is a simple tit-for-tat strategy. In this strategy, one begins by cooperating and then mimics the other player's moves. Tit-for-tat is "nice" in that it is willing to cooperate and it does not bear a grudge. It also cannot be exploited because any "defection" from cooperation will be returned.
If Ingrid uses a tit-for-tat strategy in our example above, she will work hard the first week. If she then discovers that Edward has loafed, she will loaf the next week. If, after he realizes that he cannot exploit her, he becomes ready to cooperate, a tit-for-tat strategy is ready to begin cooperating.
The power of tit-for-tat in encouraging cooperation in unusual places has been explored by Robert Axelrod in The Evolution of Cooperation (Basic Books, 1984). He argues that it could explain the many spontaneous outbreaks of "peace" in trench warfare during World War I. In the early stages of this warfare, informal and unspoken agreements often existed in which neither side would fire to kill the enemy when major battles were not under way. The best position for the soldiers on each side would have been one in which they could "exploit" the enemy by killing him with no fear of retaliation. Then, when a major battle came, the enemy would be weaker and the chances of surviving the major battle would be better. However, this was not an attainable position because the other side would retaliate.
The informal cease-fires along the front indicate the ability of cooperation to arise when no altruism at all is involved. The generals on both sides who managed the war safely behind the lines deplored the refusal of troops to kill the enemy between the ordered offenses. They could and did issue orders telling their men that killing the enemy was to be a daily affair, but they could not be sure that these orders were in fact carried out. Only by accident did they discover a way to eliminate informal peace. The British began a policy of raiding the enemy, and a raiding party was expected to bring back prisoners or to suffer deaths trying. Because there was no way to fake these results, the cooperation that had arisen between enemies collapsed.
Increasing the number of times players interact weakens the logic of the original prisoner's dilemma, but adding players strengthens it. To see this, consider the following classroom game. Your instructor divides your room into two groups. You must decide in each round of play whether to hold up a hand or a fist. Your score depends both on your decision and on how the majority of the other half of the class play. The table below shows the payoffs. Your goal is to score as many points as possible.

What will happen in this game? Perhaps you can try it and see. With most groups that play this game, only a few hands are left after three or four rounds. (Notice that the problem of the commons is identical to a prisoner's dilemma game with many people playing.)
Next we discuss two ways to coordinate economic decisions.
Copyright Robert Schenk