Investment and Government
Consumption is not the only type of spending; business spends in the form of investment, government spends, and the economy has transactions with other nations. The government also taxes. Making these adjustments to the model increases its complexity but does not change its logic.
What assumption should we make about how business makes investment decisions? We could assume that, like consumption spending, business investment decisions depend on expected income. The logic of the accelerator principle suggests this assumption. Or we could assume that the interest rate, which measures the opportunity cost of tying up assets in the form of capital, should matter. However, we will begin with the standard assumption in textbook treatments of the model: investment is determined outside the model, or in the jargon of economists, it is exogenous.
In the table below we have added investment spending to the model. At an expected income of $20,000, consumers will spend $20,000 and expect to save nothing. Business will invest $2,500. Thus actual income will be $22,500 (and actual savings will be $2,500, matching investment). Since actual income will not equal expected income, expected income should change, causing behavior to change too. Not until expected income equals $30,000 will expected income equal actual income and only then will behavior stop changing.
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
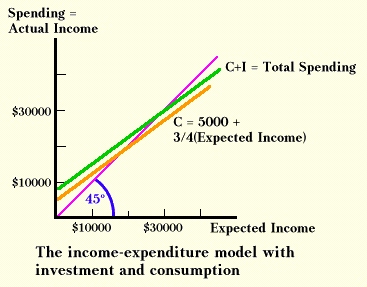
Notice that the addition of $2,500 in investment increased the equilibrium from the $20,000 to $30,000. There is a multiplier effect here, and the multiplier is four. The reason for the multiplier effect can be seen intuitively. As the result of the addition of the $2,500 in investment, actual income rises by $2,500. Expected income will also rise. But at the new expected income of $22,500, people will want to spend more than $20,000 for consumption, so there will be an additional induced increase in spending. But the story does not end here. The additional consumption increases actual and thus expected income, and changes behavior still further. The chain reaction that the addition of investment sets into effect diminishes at each step, and the total will approach $30,000.
This more complex model is illustrated graphically below. The only alteration is that the total spending line now includes investment as well as consumption. As before, the equilibrium exists when expected income equals actual income.
To complete the standard textbook model, we need to add government. Government affects the flow of spending in two ways: it adds spending in the form of government purchases of goods and services and it takes money from the flow of spending with taxes. Government purchases include payments for fighter planes, salaries of congressmen, and building of new highways. Not included in government spending are transfer payments such as Social Security payments, food stamps, or grants to needy college students. Transfers can be treated as negative taxes.
Government spending affects the model in exactly the same way as investment spending does, but the addition of taxes forces some changes in the way we have been presenting the model. Simply relabeling the table above shows the effect of adding government spending. The column titled "Investment" could be called "Investment Plus Government Spending." The column titled "Actual Income" would remain the same, but it would now be computed by adding together consumption spending, investment spending, and government spending. Because government spending enters the model in exactly the same way as investment spending, changes in it have the same multiplier effects as do changes in investment spending.
Adapting the graph to the addition of government spending is equally easy. The line in the graph above which is called "C+I" will now be called "C+I+G." Equilibrium will occur where this line crosses the 45-degree line.
Next we will add taxes.
Copyright Robert Schenk