The Production Function
When most people think of fundamental tasks of a firm, they think first of production. Economists describe this task with the production function, an abstract way of discussing how the firm gets output from its inputs. It describes, in mathematical terms, the technology available to the firm.
A production function can be represented in a table such as the one below. In this table five units of labor and two of capital can produce 34 units of output. It is, of course, always possible to waste resources and to produce fewer than 34 units with five units of labor and two of capital, but the table indicates that no more than 34 can be produced with the technology available. The production function thus contains the limitations that technology places on the firm.
Labor |
|||
Capital |
|||
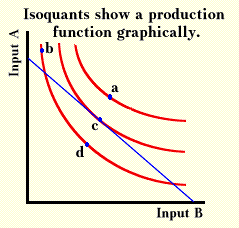
The production function can also be illustrated in a graph such as that below. This graph looks exactly like a graph of indifference curves because the mathematical forms of the production function and the utility function are identical. In one case, inputs of goods and services combine to produce utility; in the other, inputs of resources combine to produce goods or services. A curved line in the graph shows all the combinations of inputs that can produce a particular quantity of output. These lines are called isoquants. As one moves to the right, one reaches higher levels of production. If one can visualize this as a three-dimensional graph, one can see that the production surface rises increasingly high above the surface of the page; the isoquants indicate a hill. The firm must operate on or below this production surface.
There is one rule that seems to hold for all production functions, and because it always seems to hold, it is called a law. The law of diminishing returns says that adding more of one input while holding other inputs constant results eventually in smaller and smaller increases in added output. To see the law in the table above, one must follow a column or row. If capital is held constant at two, the marginal output of labor (which economists usually call marginal product of labor) is shown in the table below. The first unit of labor increases production by 13, and as more labor is added, the increases in production gradually fall.
|
|
|
The law of diminishing returns does not take effect immediately in all production functions. It is possible for the first unit of labor to add only four units of output, the second to add six, and the third to add seven. If a production function had this pattern, it would have increasing returns between the first and third worker. What the law of diminishing returns says is that as one continues to add workers, eventually one will reach a point where increasing returns stop and decreasing returns set in.
The law of diminishing returns is not caused because the first worker has more ability than the second worker and the second is more able than the third. By assumption, all workers are the same. It is not ability that changes, but rather the environment into which workers (or any other variable input) are placed. As additional workers are added to a firm with a fixed amount of equipment, the equipment must be stretched over more and more workers. Eventually, the environment becomes less and less favorable to the additional worker. People's productivity depends not only on their skills and abilities, but also on their work environment.
The law of diminishing returns was a central piece of economic theory in the 19th century and accounted for some gloomy predictions of the future. The amount of land seemed to be fixed but the number of people who could work the land was variable. If the number of people expanded, eventually adding one more person would result in very little additional food production. And if population had a tendency to expand rapidly, as some early economists believed, it followed that (in equilibrium) there would always be some people almost starving. Although history has shown the gloomy expectations wrong, the idea influenced Charles Darwin and traces of it still float around among environmentalists.
If one increases all inputs in equal proportions, one travels out from the origin on a ray. There is no law to predict what will happen to output in this case. If a 10% increase in all inputs yields more than a 10% increase in output, the production function has increasing returns to scale. If it yields less than a 10% increase in output, the production function has decreasing returns to scale. And if it yields exactly a 10% increase in output, it has constant returns to scale.
Returns to scale are important for determining how many firms will populate an industry. When increasing returns to scale exist, one large firm will produce more cheaply than two small firms. Small firms will thus have a tendency to merge to increase profits, and those that do not merge will eventually fail. On the other hand, if an industry has decreasing returns to scale, a merger of two small firms to create a large firm will cut output, raise average costs, and lower profits. In such industries, many small firms should exist rather than a few large firms.
Most products require many more than two inputs, but showing a production function with more than two inputs with graphs or tables is difficult. Products require various types of labor and capital, energy of various sorts, and raw materials. One of the key inputs, especially in larger firms, is managerial ability. Inputs do not combine by themselves to produce output. Someone must have knowledge of how to combine inputs and to coordinate the production process.
If business decision-makers lack information or are incompetent, the firm will not make the best use of available resources. Or if morale is bad in a firm, people may work poorly and produce less than they could. In either case, the firm will produce below the maximum that the production function allows. Economist Harvey Liebenstein called losses of these sorts "X-inefficiency." Although economists assume that the firm will be on the production function, a major challenge of management is to make decisions so that the firm will be on or close to the production function.
In explaining the theory of the firm, economists conventionally assume that the production function is fixed and that the firm operates on the surface of the production function. The firm need not consider the production function as fixed, but may view it as a variable that it can alter through research and development. Creativity in the form of new technology or new management techniques may loosen the boundary that the production function represents and may make possible greater profit, at least temporarily.
The second boundary that limits the firm is the demand curve for output.
Copyright Robert Schenk