Consumers' Surplus
The assumption that consumers maximize utility leads to the downward-sloping demand curve. Actually, even non-rational or random behavior will lead to a downward-sloping demand curve, as economist Gary Becker has demonstrated, but this demand curve does not have the same interpretation that a demand curve based on utility maximization (trying to attain goals) has.
Becker's argument is quite simple. Because the budget line is a constraint separating what is possible from what is not possible, even non-rational consumers face a budget constraint. Becker notes that if people randomly purchase goods, they will be randomly distributed, either along a budget constraint or within the area bordered by the budget constraint. (Becker considers both cases.) If the price of a good increases, the budget line will shift and a new random distribution of points will occur. The geometry of the situation implies that, on the average, people will buy less of a good as its price rises.
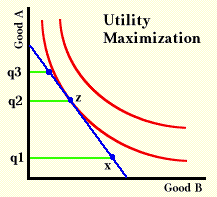
Although the demand curve of non-rational consumers will slope downward, it can no longer be interpreted as a locus of points of consumer equilibrium. With the assumption of utility maximization, the preferences and prices used to construct the graph above imply that q2 is the amount of good A that is optimal for the consumer. If either more (q3) or less (q1) is being used, there is an incentive to change behavior because it would lead to better fulfillment of goals. However, if behavior is random and not concerned with fulfilling goals, point x is as good as point z. Thus, the argument that price controls have unintended results depends on the assumption that behavior is goal-directed.
Utility maximization suggests that the demand curve, because it measures buyer's willingness to pay, shows marginal benefits to buyers. The table below indicates that people will buy only one item if the price is $5.00, or that people are willing to pay $5.00 for the first item. They are not willing to pay $5.00 for a second item, but only $4.00. A second item has a smaller marginal benefit than the first because of the law of diminishing marginal utility. The equimarginal principle suggests that as price gets lower, consumers find that they must use more of an item to keep equality among marginal-utility-to-price ratios. Alternatively, as people use more of an item, its marginal utility drops, and so must its price if they are to stay in equilibrium.
|
|
|
|
|
Willing to Buy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
This notion of the demand curve has an interesting implication known as the consumers' surplus. If in the table above consumers are buying three items, they must pay a total of $9.00. But the total value to them is $5.00 + $4.00 + $3.00 = $12.00. There is a surplus value of $3.00. In a more intuitive example, suppose that a person has been working in the hot sun all afternoon and is extremely thirsty. This person may be willing to pay as much as $2.00 for a can of cold beer, but if he can buy it for only $.50, he thinks he has found a good deal and may buy two or three. The difference between the maximum a person would pay and the actual amount that he does pay is consumers' surplus. In other words, consumers' surplus is the difference between the value in use of an item and its value in exchange.
Notice that consumers' surplus is not related to the type of surplus that occurs in a market when price is above market-clearing price. Perhaps economists would have avoided this possible confusion if they had used a term other than consumers' surplus for this concept, but they did not and the term is now well-established.
In the early days of economics people puzzled over what was called the paradox of value. This paradox disappears once we understand consumer surplus.
Copyright Robert Schenk