The Maximization Principle
Often, it is impossible or difficult to list all the options and the budget constraint as the last section does. There can be simpler ways to approach this problem. The overview suggested that we could break the question into a series of questions. We begin by assuming that all money is used to buy shirts, which, in this example, means that the person buys five shirts. Then, we ask whether the person is better off buying one hamburger than buying none. To answer this question, we need to compute the costs and benefits of making this change. Using the example from the previous section, the added benefit of the first hamburger is eight utils. To compute the cost of making this change, we must remember the budget constraint. To get a hamburger, the person must sacrifice a shirt. Because he began with five, he will be left with four. As a result, the utility he gets from shirts will decline by one util, and this is the cost of adding a hamburger. Since the change adds benefits of eight utils at a cost of one util, this is a smart change to make.
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now, we ask if another change is worthwhile. What will the costs and benefits of adding a second hamburger be? The table says that the utility of two hamburgers is 15. Because eight of those utils come from the first hamburger, the added utility of the second hamburger is seven. Because the budget constraint forces the person to give up his fourth shirt in order to obtain this hamburger, utility from shirts will drop from 31 utils to 27 utils, a loss of four utils. Thus, the benefits of adding the second hamburger are seven utils, and the cost is a loss of four utils. Adding the second hamburger is also a smart move because it increases total utility.
The third hamburger is not worth obtaining. The benefit of adding the third is six utils (moving from 15 to 21 utils in the table). But this move requires the person to move from three shirts to two, and in this move, seven utils from shirts are given up. Because the cost of adding the third hamburger (seven utils) is greater than the benefits of this hamburger (six utils), the person should not add it.
Economists call the approach taken in the preceding paragraphs the marginal approach. Thinking on the margin means that a person is asking what the effects of small changes will be. In this approach one considers marginal costs and marginal benefits. The marginal cost of a change is the additional cost caused by the change. The marginal benefit of the change is the additional benefit caused by the change. The marginal approach suggests that one should make all the changes that increase benefits more than they increase costs (or that reduce costs by more than they reduce benefits). When all these changes have been made, one will find oneself at a point for which marginal costs equal marginal benefits. This rule for finding the best level of an activity is called the maximization principle.
|
|
|||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
To see that the maximization principle does generate the largest net benefits, the problem of how many hamburgers to buy can be analyzed with total costs and total benefits. This analysis is illustrated in the table above. Columns two and three show marginal costs and benefits, and the way in which they were obtained has been described in the previous paragraphs. Total benefits of hamburgers are taken from the first table.
Total Costs are obtained from column two of the first table and depend on the budget constraint. The total cost of three hamburgers, for example, will be the lost utility of three shirts. Because five shirts give 32 utils, and losing three leaves only two giving 20 utils, the total cost of three hamburgers is 12 utils. The Net Benefit column in the second table is found by subtracting total cost from total benefit. At two hamburgers, the total utility will be ten utils higher than at the starting point of five shirts and no hamburgers.
You should see that if one has total cost one can obtain marginal cost, and if one has total benefit one can obtain marginal benefit, and vice versa. The formula for marginal cost is:
Marginal Cost = (Change in total cost)/(Change in activity)
Thus, if a business knows that the total cost of producing 98 shirts is $398 and the total cost of producing 100 is $400, the marginal cost of the 100th shirt is approximately $2/2 = $1.00. Notice that marginal cost is not the same as average cost, which is found by dividing total cost by output. Alternatively, if one knows the marginal cost or benefit, one can find the total cost or total benefit by adding up all the marginals. (Check the second table to see that this is so.)
These results can also be shown graphically. In the picture below the total costs and benefits from the second table have been graphed. The goal of the person, to maximize net benefits, requires that the person try to find the point where the total benefit curve is at its greatest vertical distance above the total cost curve. (Here is one case in which the person does not want to end up at the intersection. Can you see why?) At this point, the total cost and total benefit curves have the same slopes. Before this point, the total benefit curve is steeper, so they are moving apart. After this point, they are moving together, which means that the total cost curve has the steeper slope.
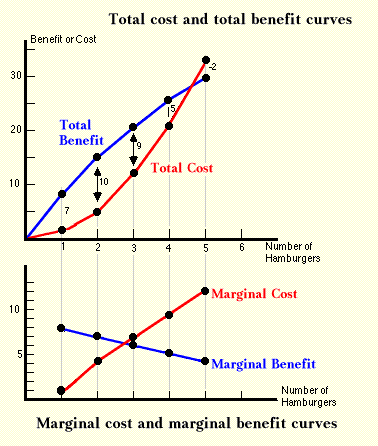
The slope of the total benefit (or cost) curve is the rise over the run, or the change in total benefit (or cost) divided by the change in the number of hamburgers. But the marginal benefit (cost) of hamburgers is also defined as the change in total benefit (cost), divided by the change in the number of hamburgers. Hence, the slope of the total benefit curve is marginal benefit and the slope of the total cost curve is marginal cost.
This idea is used to construct the marginal benefit and marginal cost curves in the bottom of the picture above. The marginal curves are obtained by graphing the slopes of the total curves. The point at which they cross corresponds to the level of activity for which the slopes of the total cost and total benefit curves are equal.
We have not exhausted the insights from this simple problem. We can also analyze the numbers with the equimarginal principle.
Copyright Robert Schenk