From Elasticity to Marginal Revenue (This is a moderately technical section that may trouble those who fear math, but it logically completes the chapter.) Marginal revenue is the extra revenue from adding another unit of output. If a firm finds that when it sells six units, its revenue is 24, and when it sells eight, its revenue is 28, its extra revenue for adding two more units is four. Its marginal revenue, or the extra revenue for adding one more unit of production, will be two. 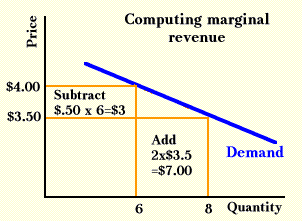The graph above illustrates an alternative way to compute this extra revenue. When the firm sells six, it can charge a price of $4, but when it sells eight, it can charge only $3.50. (Thus, six units at $4 each gives a total revenue of $24 and eight units at $3.50 each gives a total revenue of $28.) When the firm sells the extra two units, it adds two units at $3.50 each, or $7 to its revenue. However, it also loses something because it had to lower the price on the six units it was previously selling. The loss is these six units times $.5 each, or $3. The net change in revenue is $7 less $3, or $4. Equation (6) says that to get marginal revenue, the change in total revenue ($4) must be divided by the change in output (2), which in this example gives us $2. We have shown that marginal revenue can be computed as (Change in Q)P + (Change in P)Q) divided by (Change in Q). (This formula holds only approximately when changes are big, but becomes exact as the changes get very very small. Because the change in price will be negative, the second term in the numerator will be subtracted from the first.) When changes in price and quantity are very, very small, the formula for price elasticity can be written as e = ((Change in Q)/Q) divided by ((Change in P)/P) If your algebra is fairly good, you should be able to use these two formulas to show that the following equation is true: Marginal Revenue = Price (1 - 1/|elasticity|) (Verbally, this says divide one by the absolute value of elasticity. Subtract this number from one. Then, take this second number and multiply it by price. The result is marginal revenue.) This last formula says that if demand is inelastic (less than one), trying to sell more will reduce total revenue, whereas if demand is elastic (greater than one), trying to sell more will increase total revenue. This should make intuitive sense. If people are not sensitive to price, then one must reduce price a great deal to sell more, which means that total revenue declines. Copyright Robert Schenk