Monopolistic Competition
Let us continue with our example of the pushcarts, but let us change assumptions. Let the beach be very, very long, and let buyers face a cost in getting to and from the seller. To make this second assumption specific, assume that it costs buyers $1.00 to travel a mile. Finally, assume that there is one seller on the beach and that everyone values the product he sells at $10.00.
If the seller prices his product at $6.00, how many people will buy it? He should get all those people who are located less than two miles from him. To see this answer, consider someone located one mile away. This person finds that the product costs $8.00 to get because she must pay $6.00 and travel two miles (one going and one returning). Because $8.00 is less than the benefits of $10.00 she gets from the product, she will buy. If she was located three miles away, the product would now cost her $12.00 ($6.00 to the seller and $6.00 of transport costs), so she would not buy.
Now, suppose that another seller decides to locate on our very long beach. Unlike the Hotelling beach, he will not locate next to the original seller. The assumptions of transport costs and long beach change this result. In fact, the new seller should move down the beach until he has his own four-mile stretch of beach.
Suppose that both sellers are doing a great business and getting rich. Because it is very easy to roll another push cart onto the beach, the unusually high returns in this business should attract new sellers. Suppose that a new seller locates exactly two miles away from our first seller. How much of the beach will each control? If they both charge the same price, then they will evenly split the beach between them, or each will attract customers within one mile.
However, to make the story a bit more complicated, suppose that the new seller raises his price to $7.00. If the original seller still charges $6.00, then the dividing line separating customers between them will be 1.25 miles from the original seller and .75 miles from the higher-priced seller. (If you check the cost of the buyer at this point, you should see that it costs her $8.50 to go to either seller.)
In the previous example each seller has some control over price. Each realizes that if he charges a higher price, he loses some customers, but not all of them. In this way, the sellers are like monopolies: They are price searchers facing downward-sloping demand curves. However, they also are in an industry that has easy entry and exit, and as a result, there will be no long-term profits (as economists define profits) and in this way resemble price takers in perfect competition, the sellers we discussed when we drew supply curves. Because it has both elements of monopoly and competition, economists classify an industry of this type as monopolistic competition.
The model of monopolistic competition puts our situation into a more familiar form of demand and cost curves. The illustration below shows a seller with a downward-sloping demand curve and a conventional marginal cost curve. Because the demand curve slopes downward, the marginal revenue curve lies below it. The seller maximizes profit by selecting that output at which marginal revenue equals marginal costs and charges as much as he can, which is price P2. In the long run, there can be no economic profit because there is free entry into the industry. If there are any profits, others will enter the industry, positioning themselves to take away customers from the most profitable sellers. The zero profit condition implies that at equilibrium, average revenue (which is demand) must just equal average cost. When average revenue equals average cost, average profit is zero, and so total profit must also be zero.
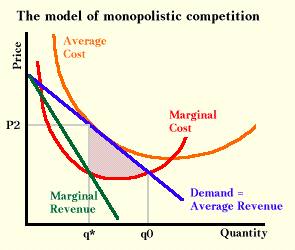
The model of monopolistic competition was considered important when it was introduced for two reasons. First, the situation it described seemed the most common form of industry. Both the single sellers of monopoly and the many sellers of price-taking competition are uncommon in comparison. Furthermore, monopolistic competition describes more than traveling costs in a geographical sense. The distance between sellers can be in the minds of buyers. Product differentiation, which results in many products that are similar but not identical, also creates a distance between products. It was this distance that seemed especially important to the developers of monopolistic competition.1
Second, notice that because price exceeds marginal cost, the graph contains a gray area of welfare loss, an unexploited value that neither firms nor customers obtain. Because monopolistic competition was seen as both common and economically inefficient, it was argued that market systems were inherently inefficient.
However, the welfare loss in the case of monopolistic competition may be illusionary. Firms could obtain this value if they could price discriminate, selling beyond q* up to qo. If they do not do so, then the resources needed to obtain the information required to price in this fashion must be more valuable than the triangle of unexploited value. Or consider possible government solutions. The problem is that sellers are too small and charge too high a price. The government could react by limiting the number of sellers and forcing them to charge lower prices. But this policy would increase traveling costs of buyers. The market may not give the optimal number of sellers (and hence the optimal distance between them), but the cost of gathering the information that would let government decide the matter is almost certainly greater than any possible welfare gain (even ignoring the political incentives that always go with government solutions).
Some economists have argued that the distance between products is often phony, that firms differentiate products to fool consumers. Their argument is surely correct in many cases. In other cases, however, product differentiation exists because it reflects differences in people's tastes. Again, there is a cost to deciding whether in each case product differentiation manipulates buyers or caters to them. It is not clear that any government policy that tries to eliminate "bad" differentiation will have benefits that exceed its costs.
When the cost of correcting a problem exceeds the possible gain from the correction, is there any real welfare loss by allowing the problem to continue? The model of monopolistic competition shows that real market systems fall short of theoretical constructs that assume away the problems of information and of making agreements among people. But any real-world system looks bad compared to theory that assumes away problems.
Finally, the theory developed above does have at least one interesting use in explaining the real world. When traveling costs are reduced, people become more price-sensitive, which means that the demand curve facing each seller gets more elastic. As a result, the marginal revenue curve shifts upward and will intersect the marginal cost curve at a higher quantity (or greater distance). For individual firms to expand sales when the industry sales are constant requires some firms to disappear. Reducing traveling costs reduces the number of firms, and development of the automobile and the highway system drastically cut traveling costs in the United States. As a result, throughout America there are thousands of villages that have completely or largely lost their retail districts.
1 While the theory of monopolistic competition suggests that there may be too much product differentiation, Hotelling's model suggests that there may not be enough.
Copyright Robert Schenk