Searching for Total Cost
Determining which level of output to produce becomes a mathematical problem when all information is known about the three constraints that the firm faces: production function, supply curves for resources, and demand curves for output. When they are not known, the problem of maximizing profit is often solved by trial and error, although an understanding of how a solution is obtained in the mathematical model with perfect information may help guide the trial-and-error process.
The maximization principle tells us that the profit maximizing level of output will be that level at which the marginal benefit to the firm of producing one more unit will just equal the marginal cost of that unit. The marginal benefit to the firm is the extra revenue from producing and selling another unit of output. This extra revenue is marginal revenue and depends only on the demand curve. The marginal cost is more complex because it depends both on the production function and the supply of resources. To discuss it, one must first compute a total cost curve for output.
Total cost depends on the prices of inputs and on the output that those inputs can produce. Suppose a unit of labor costs $12 and a unit of capital $5. Producing 27 units of output in the table below with four units of labor and one unit of capital would cost $53. However, there is a cheaper way to produce 27 because 29 can be produced with three units of labor and three units of capital for $51.
|
|
|||
|
Labor |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
Capital |
|||
There are many ways to produce most products. In the United States, farming is done with a lot of equipment and only a few people. In China, it is done with many people and few machines. A hole can be dug for a skyscraper with lots of labor and little equipment, or with little labor and a lot of equipment. Electricity can be produced from a dam that uses no fuel but a very large amount of capital, or from turbines that use a lot of fuel but little capital. However, not all of these various ways of doing things are equally cheap. What seems advantageous in one situation may not be in another where the cost of resources is different.
To find the total cost curve, we need to find the cheapest way to produce 27 units of output, 28 units of output, and all other levels of output. We begin by searching the production function for all the ways to produce 27 units of output, and then compute the cost of each of those ways. Only the cheapest of those ways will be on the total cost curve. Then, we must do the same for 28 units of output, and for all other amounts of output. When we have found the cheapest ways to produce each level of output, we will have found the total cost curve.
The total cost curve will slope upward, as in the picture below. It divides a region that is attainable from a region that is not attainable. Point a is attainable, whereas point b is not. Point a represents an expensive way to produce output. The fact that it is above the total cost curve means that a cheaper way to produce the same amount of output exists. Point b represents a method of production that does not exist. It is below the cheapest existing way to produce output.
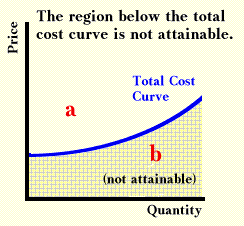
Every point on the total cost curve will satisfy the equimarginal principle of
MPA/MRCA = MPB/MRCB = MPN/MRCN
In words, the equimarginal principle says that ratios of marginal products of each resource to marginal resource cost of each resource must all be equal.1 If the ratios are equal, there is no change that could get more output at a lower cost. If they are not equal, then costs can be cut with output held constant or output can be increased with costs held constant.
A numerical example shows that if the equimarginal principle does not hold, a firm can increase output without increasing costs. Suppose that the marginal product of resource A is 10 and the firm added $5.00 to its costs to obtain the last unit of this resource. The marginal product of resource B is 9 and the firm adds $1.00 to its costs to obtain another unit. Putting these numbers into the previous equation, we see that 10/5 is not equal to 9/1. If $5.00 were shifted away from resource A, the firm would lose 10 units of output, but would gain an additional 45 if the money were used to buy more of resource B. This would give it a net gain of 35. As money is shifted, the marginal products will change until the ratios are brought into equality. (Take the time to understand this example--it is important.)
Notice that the equimarginal principle requires information from both the production function (the marginal product) and the supply curves of resources (the marginal resource costs). If the firm is a price taker in all resource markets, the marginal resource costs will be the same as the price it pays.2
1 Recall that the marginal product is the amount of extra output that an extra unit of the input would produce and that the marginal resource cost of each resource is how much the firm must pay to get one more unit of the resource. These are rough definitions--the correct mathematical descriptions are in terms of derivatives, a calculus concept.
2You may notice that one can present the discussion of the preceding paragraphs in terms of a graph that looks like an indifference curve graph. The indifference curves have become isoquants, and the budget line represents a fixed level of cost. The slope of the budget line will depend on the relative prices of resources. Output is maximized for a fixed level of expenditure at the tangency of an isoquant and the budget line; at this point the equimarginal principle holds because the slopes of the two lines are equal.
Copyright Robert Schenk