The IS Curve
In the simple income-expenditure model there was no explanation for what determined investment--it was imply assumed fixed. However, investment decisions are not arbitrary, but are determined by businessmen calculating the costs and benefits of additions to their capital stock and inventories, and by consumers calculating the costs and benefits of purchasing houses. Thus the model will be a better model if it can incorporate reasons for investment rather than leaving it outside the model.
Though the calculations determining the amounts of various categories of investment are each a bit different, all involve the interest rate. We will consider only the sort of calculation behind the decision to purchase new machinery, and will leave the decisions about inventory and housing to more advanced courses.
When a business decides whether or not to invest in new equipment, it estimates as best it can the future returns that will flow from the new equipment. Then it must compare these benefits to the costs of the investment. Suppose, for example, that a business can buy a new machine that it believes will add output worth $20,000 each year for five years. One might assume that the firm would decide to buy the machine if it costs less than $100,000. For example, if the machine costs $95,000, the firm could make a profit of $5000. However, this conclusion is wrong because it ignores the interest rate and the concept of present value.
If the firm must borrow the $95,000 in the above example and the interest rate is 10%, the machine would never earn enough to pay both the original cost and the interest on that cost. One could use the first year's returns of $20,000 to pay off part of the debt, but in the first year the amount owed would have grown by 10% or $9500. Thus after one year the business would owe $95,000-$20,000 + 9500 = $84,500. Continuing with future years, one sees that the business will lose money by purchasing the machine.
One might at this point argue that the conclusion would be different if the firm financed the machine from retained earnings. The argument is wrong. The firm has a choice of investing its $95,000 either in the machine or in a financial asset that will earn interest. Unless the firm is run by fools (in which case its future is not bright), it will use its funds where returns are highest.
In determining how much to invest, the firm must consider both the cost of the machinery and the cost of financing the investment. This latter cost depends on the interest rate. It also considers the potential returns on the investment, which depends on expected future spending in the economy. Thus in 1933, when there was massive unemployment of men and machines, there were few investment purchases which could have offered much of a return in future years. Even if the cost of financing new investment had been close to zero (it was not for most businesses, though it was for the government--interest rates that a borrower faces depend on how risky he seems to the lender), it would have made no sense for most businesses to add equipment. They already had plenty idle, and it served no purpose to build more to sit idle.
One could also argue that interest rates should affect consumption. Changes in interest rates affect the benefits from saving and the cost of borrowing. They also affect the value of financial wealth, and wealth should affect consumption. A rise in the interest rate causes the value of existing bonds to fall and a fall in the interest rate causes the value of existing bonds to rise. However, to keep the discussion simple, we will continue assuming that consumption is unaffected by changes in interest rates.
The modification that the above discussion makes to the simple income-expenditure model is illustrated below. In this table there are two columns that show investment. One column shows what investment will be at each level of income if the interest rate is 5%, while the other shows what investment will be if the interest rate is 4%. If the interest rate is 5%, equilibrium income is 600. If the interest rate drops to 4%, equilibrium income will rise to 700. Similarly, different levels of investment would exist for all other levels of interest rates, and for each interest rate, there would be an equilibrium level of income. We expect that lower interest rates would spur investment, and thus be associated with higher levels of equilibrium income.
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
When we construct a graph showing equilibrium income is for each level of interest rate, we get a curve similar to that graphed below. It is called the IS curve, and its name comes from the condition for equilibrium when there is no government in the model: investment (I) must equal savings (S).
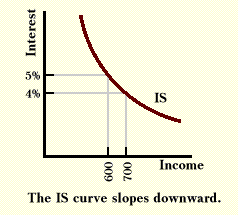
The addition of the interest rate to the income-expenditure model opens a way for monetary policy to influence spending within the logic of this model. When the central bank allows the banking system to create more money, banks increase their lending. This additional supply of funds reduces interest rates. Lower interest rates increase investment, which has a multiplier effect on total spending. A contraction of money will have opposite results.
Next we take a closer look at how money can be included in our synthesis.
Copyright Robert Schenk