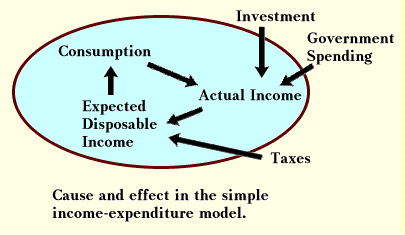
Some Different Views The feedback loop that is central in the multiplier model is illustrated below. Consumption, investment, and government spending determine actual income. Actual income and taxes determine expected disposable income, and finally expected disposable income determines what consumption will be. The feedback loop is the reason that investment and government spending have multiplier effects. A drop in investment, for example, begins by reducing actual income by the amount of the drop. Then the lower level of actual income changes expected income, and consumption also declines. Hence a $1.00 decline in investment will, according to the logic of this model, cause a decline in income of more than $1.00. We argued that the equilibrium condition for this model is that expected income equal actual income. There is another way to look at this equilibrium condition that is often useful. Expected income can be divided into three parts. First some is removed as taxes, and then what is left is divided between consumption and expected savings, or: (4) Yexp = T + C + Sexp We have also argued that actual income is made up of three types of spending: consumption, investment, and government spending, or: (5) Yact = C + I + G In equilibrium these two equation are equal, or: (6) T + C + Sexp = C + I + G Subtracting C from both sides gives us the equilibrium condition in this form: (7) Sexp + T = I + G In words, this equation says that equilibrium exists at that level of income for which the amount people intend to withdraw from the flow of spending either as taxes or savings just equals the amount they intend to add to the flow of spending as investment or government spending. 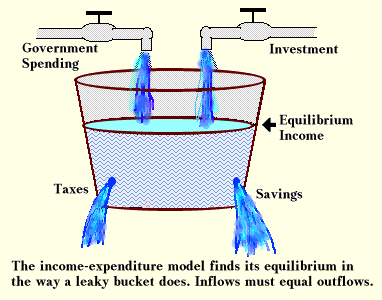This way of explaining equilibrium can be illustrated with an analogy to a leaky bucket. In the leaky bucket higher levels of water create more pressure and thus faster leakage. An equilibrium level of water occurs when the leakage just equals the inflow of water. In the multiplier model, investment and government spending are inflows and taxes and expected saving are leakages. As income increases, so does leakage in the form of expected savings. Just as there will be only one level of water in the bucket for which leakages will equal inflows, so there will be only one level of income in the model for which leakages will equal inflows. This alternative way of presenting the equilibrium condition can also be shown with graphs. In the top part of the illustration below, the difference between the C and the C+I+G lines is investment plus government spending, which the bottom part graphs separately as the I+G line. Because the distance between the C line and the C+I+G line is constant in the top part, the I+G line is flat in the bottom part. The difference between the 45-degree line and the C line is the difference between expected income and consumption, or taxes plus planned savings, which is graphed as the S+T line in bottom part. Because the C line begins above the 45-degree line, the S+T line in bottom part begins with a negative value. It rises to zero when the C line crosses the 45-degree line, and then continues to rise as the gap between the 45-degree line and the C line widens. 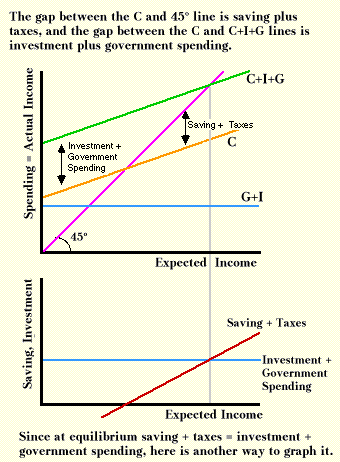Equilibrium exists when the C+I+G line crosses the 45-degree line. At this level of expected income, the distance between the C and the C+I+G lines (which is investment plus government spending) just equals the distance between the C line and the 45-degree line (which is savings plus taxes). Thus equilibrium exists when investment plus government spending equals expected savings plus taxes. Next we look at real-world implications of this model. Copyright Robert Schenk