The Simple Multiplier Model Suppose a factory with a payroll of $500,000 locates in Lemmingville, a typical suburban community. Suppose further that the $500,000 is the only money that the factory spends in the community, that all employees live in Lemmingville, and that each person who lives there spends exactly one half of his income locally. By how much will the income of Lemmingville rise as a result of the new factory? The $500,000 will be an addition to Lemmingville income. But the story does not end here because, by assumption, the people who earn the payroll will spend one half of the payroll, or $250,000, in the community. This $250,000 will become income for the shopkeepers, plumbers, lawyers, teachers, etc. Thus Lemmingville income will rise by at least $750,000. But the story does not end here either. The shopkeepers, plumbers, etc. who received the $250,000 will in turn spend one half of their new income locally, and this $125,000 will become income for other people in the community. Total Lemmingville income is now $875,000. The process will continue on and on, and as it does, total income will approach $1,000,000. Notice that the initial half million in income expands to one million once in the system. There is a multiplier effect that is similar to the multiplier effect in the model of contingent behavior. The size of the multiplier in our suburb depends on the percentage of income people spend within the community. The smaller the percentage, the more quickly the extra income leaks out of the economy and the smaller the multiplier. The Keynesian multiplier model applies to the national economy the logic by which a new factory can increase a town's income by a multiple of its payroll. Central in this model is an assumption about how people spend, the consumption function. The consumption function says that the amount people spend depends on their income, and that as income increases, so does consumption. The table below illustrates a consumption function. It says that if people expect incomes of $10,000, they will spend $12,500. This amount of spending is possible if people plan to borrow or to dissave. (To dissave means to sell assets.) The table says that when expected income is $30,000, people will spend $27,500, which means that they plan to save $2,500. Table 1: A Consumption Function Expected Income Consumption Expected Savings $10,000 $12,500 -$2,500 12,000 14,000 -2,000 20,000 20,000 0 30,000 27,500 2,500 The table shows that if expected income rises by $2,000, from $10,000 to $12,000, people will increase their spending by $1,500, or that they will only spend three-fourths of additional income that they expect to receive. This fraction of additional income that people spend has a special name, the marginal propensity to consume (or mpc for short). In the table above the mpc is always three-fourths. Thus if income increases by $8000, from $12,000 to $20,000, people increase spending by $6,000, from $14,000 to $20,000. The marginal propensity to consume can be computed with the formula: (1) MPC = (change in consumption) divided by (change in income) In addition, economists often talk of the marginal propensity to save, which is the fraction of additional income that people save. Since people either save or consume additional income, the sum of the marginal propensity to save and the marginal propensity to consume should equal one. The value of the marginal propensity to consume should be greater than zero and less than one. A value of zero would indicate that none of additional income would be spent; all would be saved. A value greater than one would mean that if income increased by $1.00, consumption would go up by more than a dollar, which would be unusual behavior. For some people a mpc of 1 is reasonable, meaning that they spend every additional dollar they get, but this is not true for all people, so if we want a consumption function that tells us what people on the average do, a value less than one is reasonable. 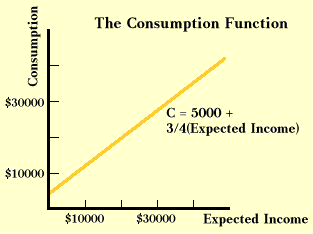The consumption function can also be illustrated with an equation or a graph. The equation that gives the consumption function in the table above is: (2) Consumption = $5000 + (3/4)(Expected Income). If people expect an income of $10,000, this equation says consumption will be: (3) Consumption = $5000 + (3/4)($10000) = $5000 + $7500 = $12500 which is the same result that the table contains. Notice that one can see the marginal propensity to consume in this equation. It is the fraction 3/4. Graphing the consumption function presented above in the table and equation yields a straight line with a slope of 3/4 shown below. If the slope of the consumption function, which is the mpc, never changes, the consumption function is linear. If the mpc changes as income changes, then the consumption function will be a curved line, or a nonlinear consumption function. The $5,000 term in equation 2 is shown on the graph as the intercept, which indicates the amount of consumption if expected income is zero. 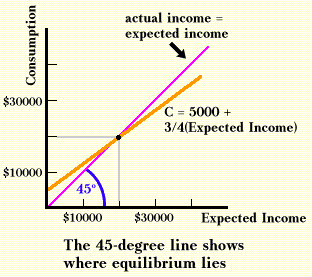When will this model be in equilibrium? To answer this, recall that spending by one person is income for another. Because so far we have assumed that consumption is the only form of spending, the amount of consumption spending will equal actual income. If people expect income of $10,000 and spend $12,500, actual income will exceed expected income. It is reasonable to suppose that as a result people will change their expectations, and thus their behavior. The logical equilibrium condition in this model is that expected income should equal actual income. In the table we see that $20,000 will be equilibrium income. When people expect income to be $20,000, they act in a way to make their expectations come true. We can show the solution on a graph by adding a line that shows all the points for which actual income equals expected income. These points will form a straight line that will bisect the graph, shown below as a 45-degree line. Equilibrium income occurs in the model when the spending line intersects the 45-degree line. It is relatively simple to add business and government spending to this model. Copyright Robert Schenk