Answers: Correlation 1
1. A sociology student is examining the relationship between number of siblings and achievement in school. She has the computer calculate a correlation, and notices that under the correlation coefficient the computer has given the observed level of significance of .94. True or false and explain: She should conclude that this result does not look random and therefore it seems that the number of siblings affects school achievement.
False. The results appear to be random. It is the level of significance that is high, not the correlation coefficient. A level of significance of .94 means that if we were correlating sets of random numbers, 94% of the time we would get correlation coefficients as large as or larger than she is getting if we had the same number of observations.
2. An instructor is curious to see how the test scores of his students are related to the amount of homework they do. Homework scores depend only on whether or not the student completes the assignment, while test scores depend on the number of questions a student answers correctly. He performs a correlation between test scores and homework points and finds:
r = -.650; level of significance = .000; N = 42.
Which of the following should he conclude and why?
- a) Students who do poorly on tests tend to skip homework.
- b) Students who do well on tests tend to skip homework.
- c) There is no real relationship between how well students do on tests and how much homework they do.
He should conclude that students who do well on tests tend to skip homework because the correlation is negative. It may suggest that homework is not effective. The level of significance says that the probability of getting this sort of result by random chance is less than one in a thousand, so he will believe that he has found something real.
3. "For boys, frequent weigh-ins didn't lead to weight gain, the study found. Boys who weighed themselves often were more likely than other boys to take unhealthy measures to control their weight, but the difference was too small to be considered statistically significant." These sentences are taken from a news report found on the Internet. Explain what the second sentence means in language that would be understandable to someone who has not had a course in statistics.
The second sentence means that even though there was a slight correlation, it was small enough so that we would expect to get similar results quite often by random chance. The way this is reported is misleading to anyone who does not understand statistics. The article is presenting a result that is not supported. The level of significance says that you cannot conclude that boys who weighed themselves often took unhealthy measures to control their weight.
4. A correlation was run between age of students and their GPA and the results are shown below.
AGE
GPA
AGE
Pearson Correlation:
Sig (2-tailed):
N:1.000
50-.031
.829
50GPA
Pearson Correlation:
Sig (2-tailed):
N:-.031
.829
501.000
50
- a) What does the correlation in the above table tell you about GPA and age in this sample?
- b) What can you infer about GPA and age in the population? Explain.
- c) The sign of the correlation coefficient is negative. What does a negative sign indicate?
- d) Using the tables at the back of the book, how big would the correlation have to be before we could be confident that there was some meaningful relationship between age and GPA in the population? Explain.
a) It is close to zero. If
you plotted the results on a scatter diagram, you would not
see any relationship.
b) Nothing. If you correlating 50 pairs of random numbers,
almost 83% of the time you will get correlation coefficients
that are further from zero than -.031. This is the sort of
result you would expect to get if the true correlation is
zero.
c) A negative sign indicates an inverse relationship. Higher
age means smaller GPA. But see a and b above.
d)
5. A researcher interested in what characteristics were correlated with student use of computer-assisted lessons found a correlation of .4153 between the number of lessons a student took and the student's high-school grade-point average.
- a) How would you explain in words what this number tells us?
- b) The researcher computed a t-value of 4.7 with 104 degrees of freedom for this correlation. Can the researcher conclude with confidence that these lessons will tend to be used more by students with higher high-school grades? Explain.
a) Students who had high
high-school grades tended to use the computer-assisted
lessons more and students with low high-school grades tend
to use the lessons less, but there were many exceptions.
b) The result does not appear to be random chance. It
appears that there is a real relationship here. However,
there is no information about what is cause and what is
effect.
6. We expect that as cars get older and have more miles, their value will decrease. We can check this expectation in a preliminary way with correlation. Taking a sample of Cadillacs listed for sale in the want ads of a large city paper, I fed their prices, ages, and mileage into a statistical computer program and got the following results:
|
PRICE |
MILES |
AGE |
YEAR |
||
|
PRICE |
Pearson Correlation: |
1.000 |
-.777 |
.870 |
870 |
|
MILES |
Pearson Correlation: |
-.777 |
1.000 |
.593 |
-.593 |
|
AGE |
Pearson Correlation: |
.870 |
.593 |
1.000 |
1.000 |
|
YEAR |
Pearson Correlation: |
870 |
-.593 |
1.000 |
1.000 |
- a) How many observations do I have?
- b) Why is the correlation between Year and Age -1.000?
- c) Why is the correlation between age and miles positive while the correlation between age and price negative?
- d) All the significance levels are .000. What does that tell us?
a) 34. N is the number of
cars included in the study.
b) Because Age is found by subtracting the year of the car
from the current year. As the year of the car goes up, the
age goes down, a negative relationship.
c) Older cars tend to have more miles on them, a positive
relationship. As cars get older, their value decreases, a
negative relationship.
d) The results are not random. Cars really do lose value as
they get old. And newer cars really do have fewer miles on
them than older cars. Correlation shows something that was
obvious all along.
7. Suppose we are interested in the correlation between last year's income and this year's income for a group of people.
- a) If the correlation between last year's income and this year's income is one, does it follow that everyone in the group earned the same in both years?
- b) Suppose that the correlation between last year's income and this year's income is zero. If we know what people earned last year, will this information give us any help in predicting what their income is be this year? Explain.
- c) Suppose we get these data:
Person Income Last Year Income This Year A
$26,000
$26,000
B
$40,000
$20,000
C
$12,000
$36,000
D
$20,000
$20,000
E
$14,000
$27,000
- Would the correlation coefficient of these numbers be positive, negative, or zero? (You do not have to compute the correlation coefficient to answer this.) Explain.
- d) Suppose that people who earned a lot last year tend to earn a lot this year and people who earned little last year tend to earn little this year. However, there are a few exceptions, people who had a bad year followed by a good year or vise versa. What range of correlation coefficients would capture this association between last year's income and this year's income? Explain.
a) No. If everyone earns 90%
of what they earned last year, the correlation will still be
one.
b) If the correlation is zero, there is no relationship
between what people earned last year and what they earned
this year.
c) It will be negative because the two who earned little
last year earned more than average this year, and the one
person who had a high income last year has one of the lowest
incomes this year.
d) If most people repeat their income from one year to the
next with a few exceptions, the correlation will be
positive, but the exceptions will drive us away from one. So
somewhere between .3 and .8.
8. Otto Mobile collects data from 25 cars. He then computes a correlation between weight of the car and its gas mileage. The answer he arrives at is -1.4. Interpret.
He made a mistake. Correlation cannot be less than -1.
9. Brandon Cumber takes 50 numbers from a table of random numbers. He calls the first 25 the X variables and the second 25 the Y variables and computes a correlation. Computing a t-value from the formula t=(r-0)/(standard error of p) he gets 2.102 with 23 degrees of freedom. He therefore claims that he has conclusively proven that either the procedure does not work as advertised or that the table of numbers is not random. Evaluate his claim.
About 5% of the time you will get a t-value either greater than 2 or less than -2. By random chance he seems to have gotten one of those results that will happen one time in twenty. And in this case we can be sure it is random chance because he was using random numbers.
10. Doyle Zirkle is certain that there is a relationship between the kind of clothes people wear and their personalities. He has heard that correlation is a way of measuring how strong relationships are so he asks you to help compute a correlation to prove that he is correct. Assuming you want to help him, what should you say or do?
To compute a correlation coefficient, you have to be able to measure what it is that you are studying. How do you measure personality or clothing style? You might be able to classify them, which would allow you to use some other statistical procedure, such as Chi-square.
11. There is a relationship between X and Y on the graph below. However, the correlation coefficient will be close to zero. Explain why and illustrate on the graph.
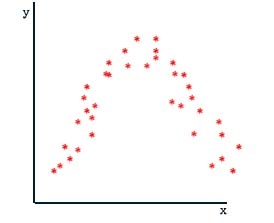
It is important to always be aware that correlation measures linear relationships. There is a relationship here, but it is not linear.